進化の激しいクラウド業界で活躍し続けるためには、業務で扱う技術への理解を深めることが欠かせません。そのためにも、エンジニアリングの基礎としてコンピューターサイエンスを学ぶことの重要性はますます高まっていると感じています。
今回ご紹介する「グラフ理論」は、コンピューターサイエンスの中でもネットワークの構造をモデル化し、数学的に分析するための重要なツールとして、広く活用されています。
本記事では、グラフ理論の基礎を成す「最短経路問題」を取り上げ、その代表的な解法である「ダイクストラ法」について、具体例を交えながら、初めての方でもわかるように紹介します。
この記事で扱うこと
- 最短経路問題の概要
- ダイクストラ法の考え方と手順
この記事で扱わないこと
- アルゴリズムの数学的な証明
最短経路問題とは
グラフ理論における最短経路問題とは、重み付きグラフの与えられた2つのノード間を結ぶ経路の中で、重みが最小の経路を求める最適化問題です。
「重み」とは、グラフの頂点と頂点をつなぐ辺の「コスト」「距離」「容量」など、様々な意味を持ちます。
ダイクストラ法とは?
ダイクストラ法とは、始点から最も近い頂点から順に、最短経路を確定していくアルゴリズムです。
ダイクストラ法の手順
前提条件
- グラフは頂点(ノード)と辺(エッジ)で構成される重み付き有向グラフとする
- 辺の重みは全て非負とする
- 始点①から終点④までの最短道を求める
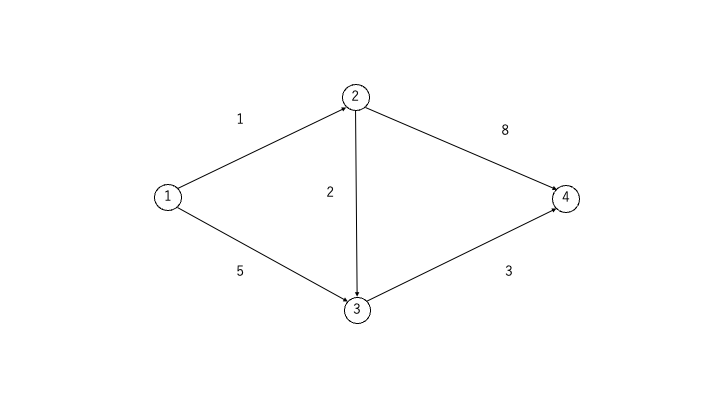
STEP0:重み付き有向グラフを用意
まず、以下のような重み付き有向グラフを考えます
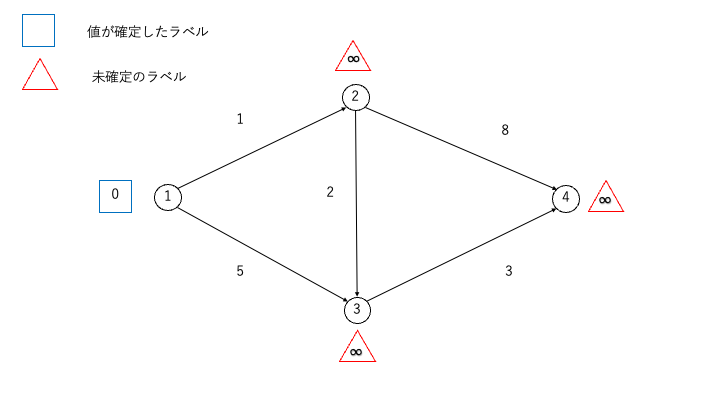
STEP1:ラベルの付与
- 始点(①)には「ラベル0」を付与します
- 他のすべての頂点(②, ③, ④)には「一時ラベル ∞」を付与し、初期化します
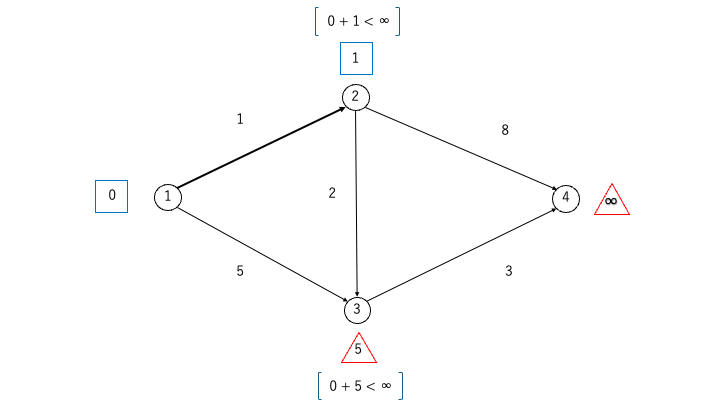
STEP2:ラベルを更新
次に、現在ラベルが確定している頂点(この時点では①)から、未確定のラベルが付いている直接つながる頂点(②、③)に対して、次の更新式が成り立つならばラベルを更新します:
更新式:現在のラベル + 次頂点をつなぐ辺の重み < 次頂点のラベル
- ①→②の場合、0 + 1 = 1 < ∞なので頂点②のラベルを1に更新します
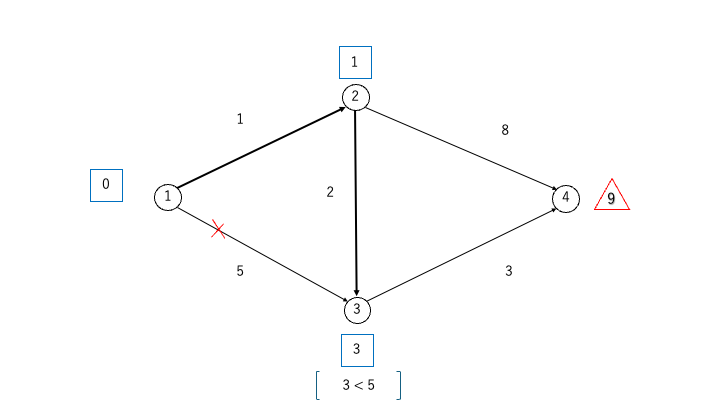
STEP3:最小のラベルを持つ頂点を選択し、再度ラベルを更新
- この時点で最小のラベルを持つ頂点である②を選択します
- 頂点②と隣接する頂点に対して、STEP2と同様にラベルを更新できるか確認します
STEP4:終点④のラベルが確定するまでラベルの更新を繰り返す
- 上記のSTEP2とSTEP3を、終点④のラベルが確定するまで繰り返します
- この際、最適な経路に使用されないとわかった時点でいらない辺は破棄します
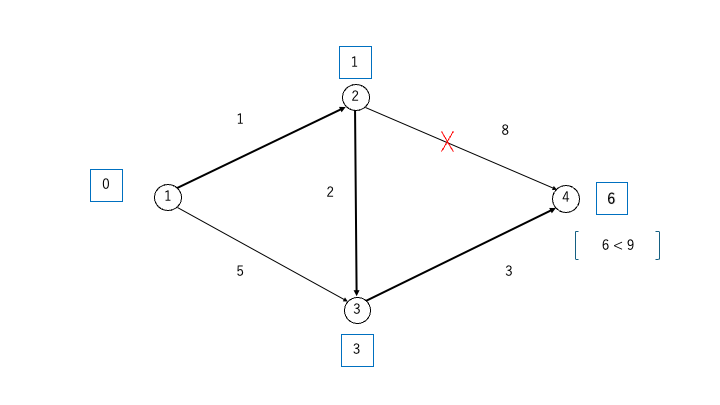
STEP5:結果
- 始点①から終点④までの最短経路は①→②→③→④であることが求められました
まとめ
本記事では、グラフ理論の基礎的なアルゴリズムであるダイクストラ法を用いた、重み付き有向グラフの最短経路を求める方法を紹介しました。
ダイクストラ法は最短経路問題を解決する強力なアルゴリズムですが、負の重みを持つ辺が存在するグラフでは、正しく最短道を求めることができないという制約を抱えています。
次の記事では、負の重みを持つグラフの最短道を求める際に利用されるアルゴリズム、「ベルマン・フォード法」を紹介します。
最後までお読みいただきありがとうございました!


