前の記事では、最短経路問題を解くための基礎的なアルゴリズムであるダイクストラ法について紹介しました。
ダイクストラ法には、負の重みを持つ重み付きグラフを正しく扱えないという欠点がありました。

参考：[はじめてのグラフ理論]ダイクストラ法で最短経路を見つける

本記事では、負の重みを持つ重み付きグラフの最短道を導く際に有効なアルゴリズムであるベルマン・フォード法を紹介します。
ちなみに、ベルマン・フォード法は通貨の裁定取引などに使用されているようです。

この記事で扱うこと

  • ベルマン・フォード法の考え方と手順

この記事で扱わないこと

  • ベルマン・アルゴリズムの数学的な証明

ベルマン・フォード法とは

ベルマン・フォード法は、辺の重みに負の値が含まれるグラフにおける、始点から終点への最短経路を導くアルゴリズムです。

ベルマン・フォード法の手順

前提条件

  • グラフは頂点（ノード）と辺（エッジ）で構成される重み付き有向グラフとする
  • 辺の重みに負の値が含まれる
  • 始点①から終点④までの最短道を求める

STEP0：負の重みを持つ重み付き有向グラフを用意

STEP1：ラベルの付与

  • 始点①にラベル0、他の全ての頂点（②, ③, ④）には一時ラベル∞を与えます
  • Sは直前の手順でラベルが更新された頂点の集合とします

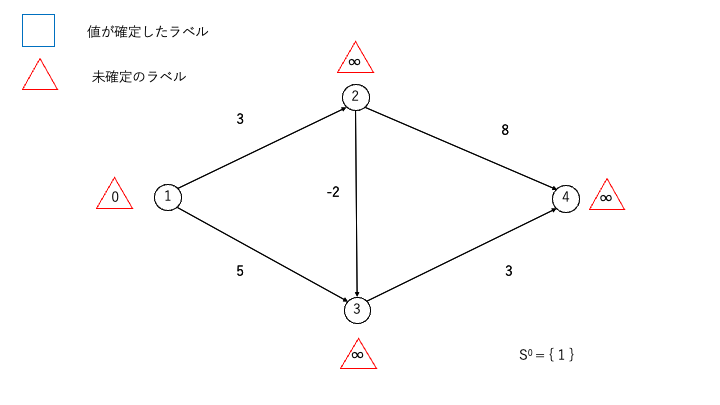
STEP2：ラベルを更新

ダイクストラ法と同様、始点①から到達可能な頂点において、次の更新式が成り立つならば次点のラベルを更新します

更新式：現在のラベル + 次頂点をつなぐ辺の重み < 次頂点のラベル

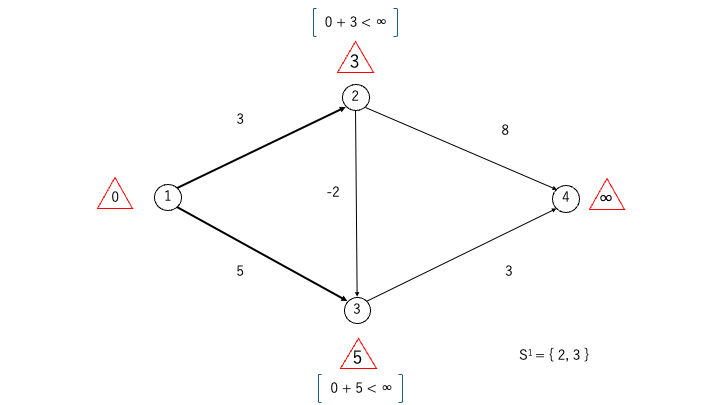
  • 頂点①→頂点②：0 + 3 = 3 < ∞なので、②のラベルを更新します
  • 頂点①→頂点③：0 + 5 = 5 < ∞なので、③のラベルを更新します
  • 頂点②と③のラベルが更新されたので、S¹ = { 2, 3 }となります

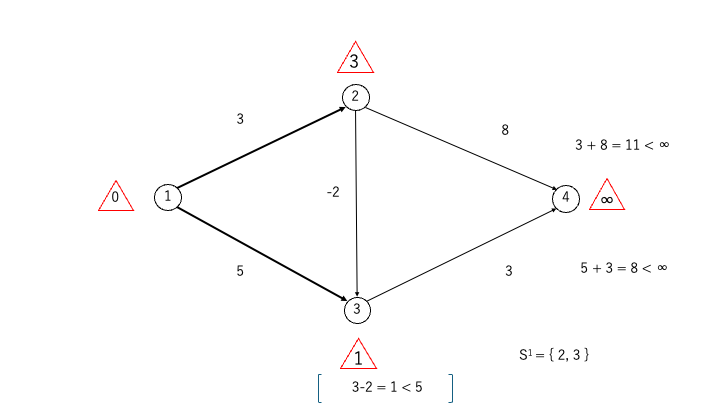
さらに、②と③から伸びる辺を調べてラベルを更新する

  • 頂点②→頂点④：3 + 8 = 11 < ∞
  • 頂点②→頂点③：3 – 2 = 1 < 5（ラベルを更新）
  • 頂点③→頂点④で5 + 3 = 8 < ∞

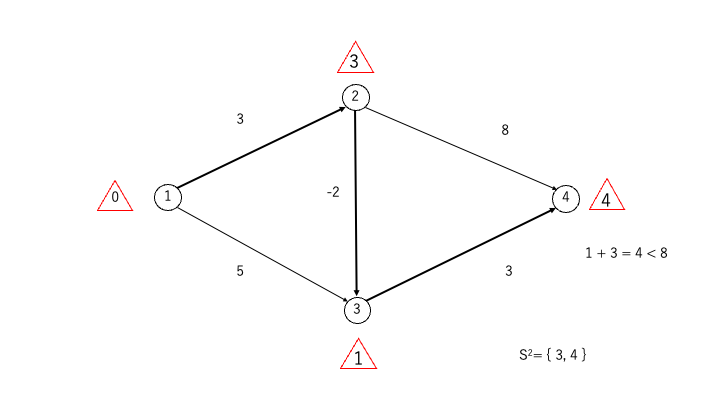
さらに、頂点③から伸びる辺を調べてラベルを更新する

  • 頂点③→頂点④：1 + 3 = 4 < 8（ラベルを更新）

STEP3：全てのラベルが変化しなくなった時点で終了

  • 全ての辺を調べてもラベルが更新されない状態になったら、最短経路が確定します

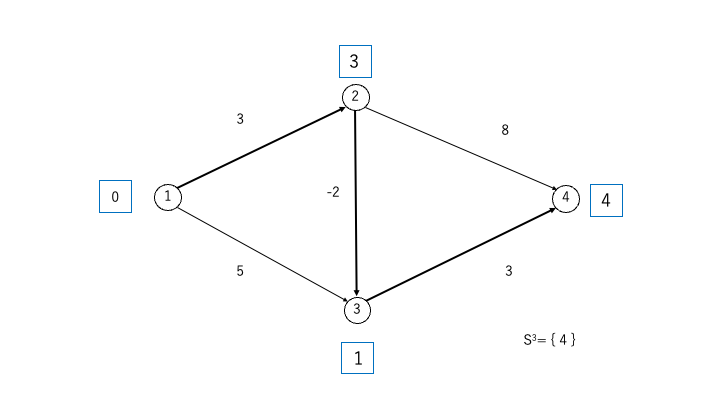
STEP4：結果

  • 始点①から終点④までの最短経路は①→②→③→④であることが求められました

まとめ

本記事では、ベルマン・フォード法を用いて負の重みを持つ有向グラフの最短経路を求める方法を紹介しました。
最短経路問題を解く手順はダイクストラ法と似ていますが、各頂点のラベルは最後まで一時ラベルであることに注意が必要です。

次回は最大フロー問題を解くためのアルゴリズムである「フォード・ファルカーソン法」を紹介します。

最後までお読みいただきありがとうございました！