これまでの記事では、最短経路問題を解くために使用されるアルゴリズムであるダイクストラ法、そして負の重みを持つグラフにも対応できるベルマン・フォード法について紹介してきました。

参考：
[はじめてのグラフ理論]ダイクストラ法で最短経路を見つける
[はじめてのグラフ理論]ベルマン・フォード法で最短経路を見つける

本記事では、グラフ理論におけるもう一つの重要な問題である「最大フロー問題」を解くためのアルゴリズム、「フォード・ファルカーソン法」に焦点を当て、その考え方と手順を具体例を用いて紹介します。

この記事で扱うこと

  • 最大フロー問題の概要
  • フォード・ファルカーソン法の考え方と手順

この記事で扱わないこと

  • アルゴリズムの数学的な証明

最大フロー問題とは

グラフ理論における最大フロー問題とは、各辺に容量制限のあるグラフにおいて、単一の始点（ソース）から単一の終点（シンク）の間に流れるものの最大量を求める問題です。

フォード・ファルカーソン法とは

フォード・ファルカーソン法は、フローネットワークにおいて、残余容量が存在する限り、増加道に沿ってフローを増加させ続けることで、最大フローを導くアルゴリズムです。

  • 残余容量：辺において、あとどれくらいフローを流せるかを表す値。例えば、辺の容量が10で、現在7のフローが流れているなら、残余容量は3となる
  • 増加道：残余容量が0でない道を繋いで、始点から終点まで到達できる道
  • 残余ネットワーク：各辺の容量を、残余容量を用いてモデル化したネットワーク

フォード・ファルカーソン法の手順

前提条件

  • グラフは頂点（ノード）と辺（エッジ）で構成される容量付きグラフとする
  • 各辺の容量は全て非負とする
  • 始点①から終点④までの最大フローを求める

STEP0：容量付きグラフを用意

  • まず、以下のような容量付きグラフを考えます

 

STEP1：増加道を見つけ、その辺に沿って流せるだけフローを流す

  • 増加道、頂点①→頂点②→頂点③→頂点④を考えます
  • 流すフローは、min {5, 3, 4}となります
  • 次の図は、頂点①→頂点②→頂点③→頂点④へフロー3を流した後の残余ネットワークです

 

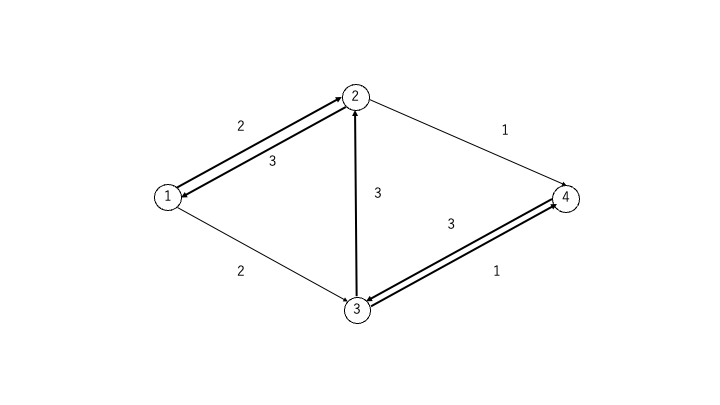
STEP2：フローが流せなくなるまでSTEP1の操作を続ける

  • 続いて、頂点①→頂点③→頂点④へ流量1を流します

 

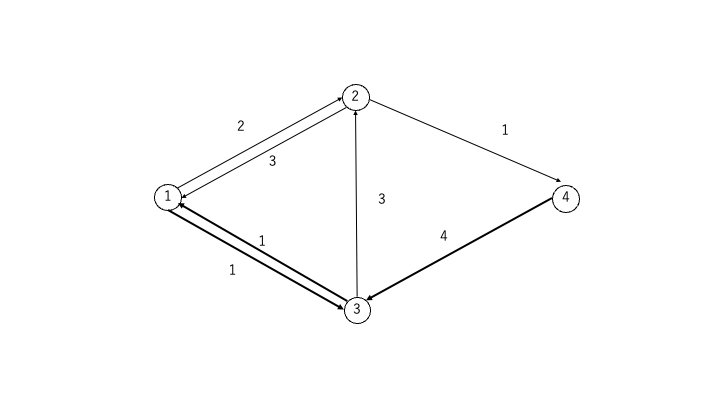
  • 最後に、頂点①→頂点②→頂点④へ流量1を流します

 

STEP3：結果

  • 始点①から終点④までの増加道がなくなったので、ここで操作を終了します
  • 各ステップで流した流量を合計すると、3 + 1 +1 = 5 となり、最大フローは5であることが導かれました

まとめ

本記事では、フォード・ファルカーソン法を用いてグラフ内を流れる最大フローを求める方法を紹介しました。

次回は、最小費用フロー問題を解くための、フォード・ファルカーソン法を拡張したアルゴリズム、「バサッカー・ゴーウェン法」を紹介します。

最後までお読みいただきありがとうございました！