これまでの記事では、最短経路問題を解くためのダイクストラ法、負の重みを持つグラフに対応可能なベルマン・フォード法、そしてネットワークにおける最大フローを求めるフォード・ファルカーソン法について紹介してきました。

参考：
[はじめてのグラフ理論]ダイクストラ法で最短経路を見つける
[はじめてのグラフ理論]ベルマン・フォード法で最短経路を見つける
[はじめてのグラフ理論]フォード・ファルカーソン法で最大フロー問題を解く

本記事では、「最小費用フロー問題」を解くためのアルゴリズムであり、前回紹介したフォード・ファルカーソン法を拡張した「バサッカー・ゴーウェン法」(Busacker & Gowen algorithm)に焦点を当て、具体例を用いながら基本的な考え方を紹介します。

この記事で扱うこと

  • 最小費用フロー問題の概要
  • バサッカー・ゴーウェン法の考え方と手順

この記事で扱わないこと

  • アルゴリズムの数学的な証明

最小費用フロー問題とは

最小費用フロー問題とは、各辺に容量と品物を運ぶための単位あたりの費用を付与したネットワーク上で、ある一定のものを運ぶときにかかる費用を最小化するようなフローを見つける問題のことです。

バサッカー・ゴーウェン法とは

バサッカー・ゴーウェン法は、フォード・ファルカーソン法を拡張したアルゴリズムで、 コストも考慮して増加道を選択するといった手法をとります。

バサッカー・ゴーウェン法の手順

前提条件

  • 流量と単位あたりコストが設定された有向グラフを考える
  • 始点から終点までフローを流すのにかかる費用を最小化する
  • 流量は5で固定する

STEP0：流量と単位あたりコストが設定されたグラフを用意

各辺に[流量, 単位あたりコスト]を設定します

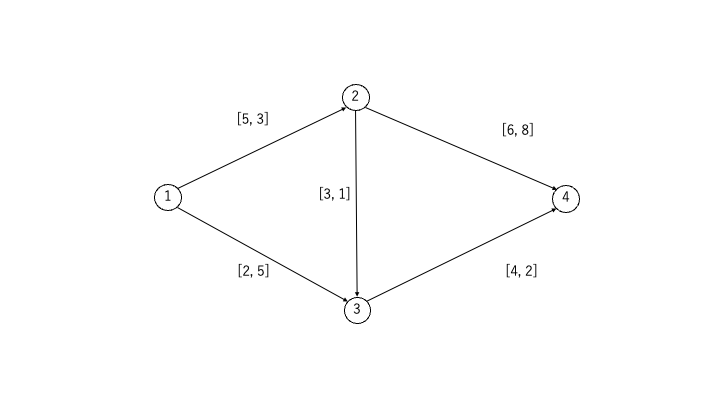
STEP1：始点から終点までの増加道のうち、コストが最小のものを選択

コストが最小となる増加道「頂点①→頂点②→頂点③→頂点④」を選択し、フォード・ファルカーソン法と同様、フローを目一杯3流し、残余ネットワークを作成します

  • 頂点①→頂点②→頂点④のコスト：3 + 8 = 11
  • 頂点①→頂点②→頂点③→頂点④のコスト：3 + 1 + 2 = 6
  • 頂点①→頂点③→頂点④のコスト：5 + 2 = 7

 

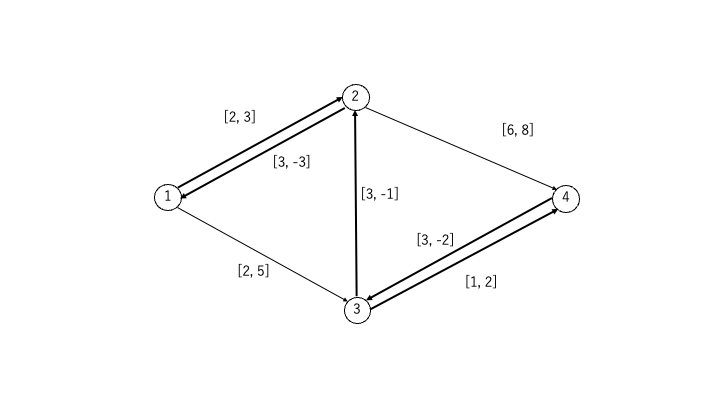
STEP2：流量のキャップに達するまでSTEP1と同様の操作を繰り返す

コストが最小となる増加道「頂点①→頂点③→頂点④」を選択し、フローを1流します

  • 頂点①→頂点②→頂点④のコスト：3 + 8 = 11
  • 頂点①→頂点③→頂点②→頂点④のコスト：5 – 1 + 8 = 12
  • 頂点①→頂点③→頂点④のコスト：5 + 2 = 7

 

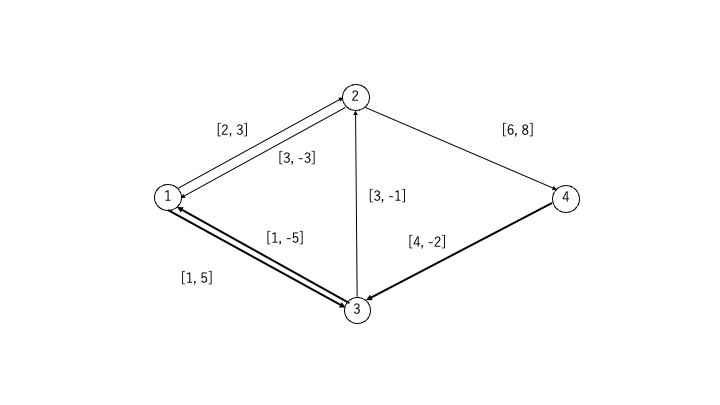
STEP3：流量のキャップに達する

コストが最小となる増加道「頂点①→頂点②→頂点④」を選択し、フローを1だけ流せば固定流量5(= 3 + 1 + 1)に達するため、ここで操作を終了します

  • 頂点①→頂点②→頂点④のコスト：3 + 8 = 11
  • 頂点①→頂点③→頂点②→頂点④のコスト：5 – 1 + 8 = 12

 

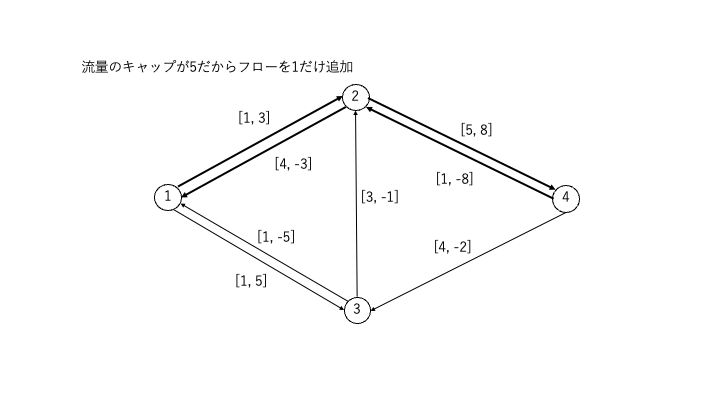
STEP4：結果

  • 固定流量5に到達し、最小費用フローを得ることができました。図における各辺のラベルは(流量 / コスト)を表します

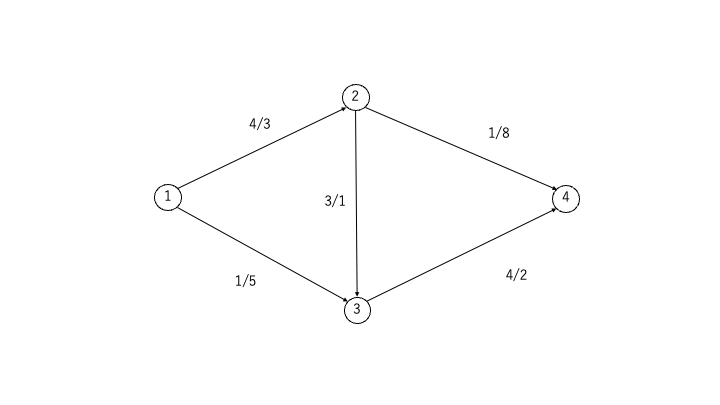
まとめ

本記事では、バサッカー・ゴーウェン法を用いて、各辺に容量とコストが設定されたネットワークにおける最小費用フロー問題を解く方法を紹介しました。

最後までお読みいただきありがとうございました！